Als u de eerdere afleveringen hebt gelezen dan zal het inmiddels tot u zijn doorgedrongen (voor zover dat nog niet het geval was) dat opties nogal complexe instrumenten zijn, en dat die complexiteit nog aanzienlijk toeneemt als we bepaalde optieposities met elkaar combineren in een optiestrategie.
De optiebelegger heeft daarom een geavanceerd instrumentarium nodig om snel beslissingen te kunnen nemen in de optiewereld. Zo’n instrumentarium is er, we zouden het de optie cockpit kunnen noemen, omdat het een aantal moeilijk grijpbare begrippen in heldere getallen weergeeft. Het loont om zich meester te maken van dit instrumentarium, zodat beginnersfouten kunnen worden vermeden en u als een volleerd optiehandelaar in uw cockpit plaats kunt nemen.
We moeten wel wijzen op het feit dat deze instrumenten niet zaligmakend zijn en niet alles zeggen. Grote wendingen in de markt kunnen ook de meest uitgedokterde en uitgebalanceerde optiestrategie een loer draaien en menig parameter in het zand doen bijten. Na deze relativerende opmerking gaan we ons instrumentarium, bestaande uit een groot aantal Griekse letters, introduceren.
Instrumentarium voor beleggen in opties
De Delta
De delta van een optie, of een combinatie aan opties, meet hoe de optie reageert op een verandering van de onderliggende waarde. At the money (ATM) calls of putopties hebben doorgaans een delta van rond de 0,5, dat wil zeggen, als de onderliggende waarde 1 punt stijgt, dan stijgen de calls (dalen de puts, deze hebben strikt gezien een negatieve delta) 0,5 punten.
De delta kan variëren van 0 tot 1 (voor puts van -1 tot 0). Een delta van 1 wil zeggen dat de optie zich gedraagt als de onderliggende waarde, elke stijging (of daling) van de onderliggende waarde kunnen we cent voor cent terugvinden in de verandering van de optieprijs. Dit artikel is slechts een overzicht, maar als we het over de delta in een aparte verhandeling hebben dan zullen we laten zien hoe deze met name in gecombineerde optiestrategieën is te gebruiken.
De Vega
Opties reageren niet alleen op veranderingen in de prijs van de onderliggende waarde, ze reageren ook op veranderingen in de geïmpliceerde volatiliteit van de onderliggende waarde, en deze is aanzienlijk minder goed waarneembaar. Vandaar dat het handig is om hier een parameter voor te hebben, en dat is de vega.
Dit is handig, omdat sommige optiestrategieën lang zijn in volatiliteit. Dat wil zeggen dat de netto positie toeneemt in waarde als de geïmpliceerde volatiliteit van de onderliggende waarde. Andere optiestrategieën zijn juist volatiliteit neutraal, of zelfs short. Simpele gekochte calls en puts zijn bijvoorbeeld long op de volatiliteit, de optiepremies nemen in waarde toe als de geïmpliceerde volatiliteit van de onderliggende waarde toeneemt.
De vega is simpel een maatstaf voor de sterkte van dit effect. Voor alle opties is deze positief, de optiepremies nemen toe bij een toename van de volatiliteit in de onderliggende waarde, maar bij optiestrategieën kunnen ook opties worden verkocht waardoor de vega negatief kan worden als we de strategie als geheel beschouwen (we hebben het dan over de vega van de positie).
De Theta
De theta meet wat elke optiebezitter al eens aan den lijve heeft meegemaakt, de frustrerende leegloop aan optiepremie bij het naderen van de expiratiedatum. Dit geldt natuurlijk vooral voor out of the money (OTM) opties, waar de premie slechts bestaat uit tijdswaarde en geïmpliceerde volatiliteit, en deze verdampen geheel bij expiratie out of the money.
De theta meet dit tijdswaarde verlies, en is dus altijd negatief (we hebben het hier niet over de netto theta van een gecompliceerde samengestelde optiepositie, welke ook positief kan zijn). De bezitters van opties denken dat de delta de theta kan verslaan, dat wil zeggen, dat de onderliggende waarde sneller in hun voordeel verandert dan dat de tijdswaarde uit de optie loopt. Dit wil nog wel eens tegenvallen.
Vandaar dat u ook de rollen om kunt draaien, en opties kunt schrijven. U profiteert dan van de theta, aangezien de tijdswaarde langzaam uit de optie loopt en als de onderliggende waarde niet te veel in een voor u ongunstige richting beweegt kunt u de opties goedkoper terug kopen, of zelfs waardeloos laten aflopen. Theta wint het dan van delta.
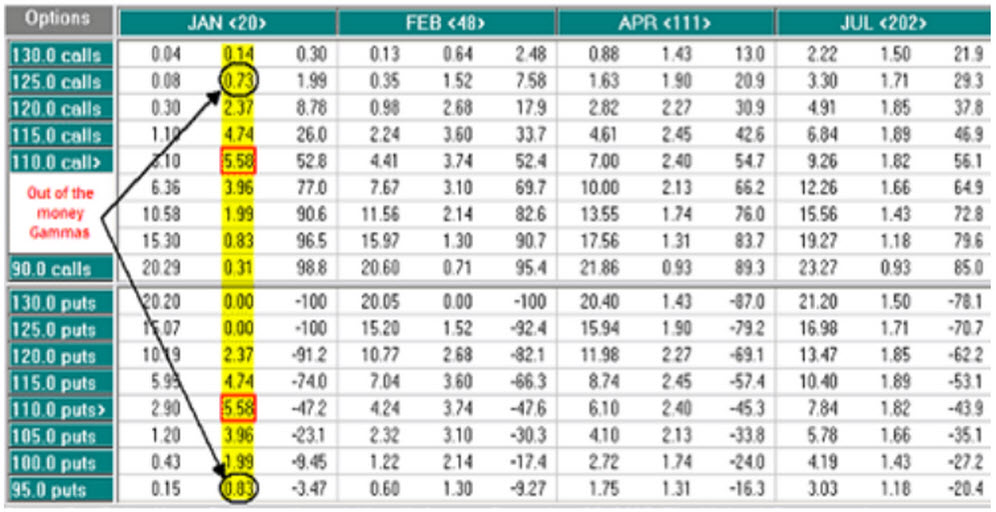
De Gamma
We weten dat de delta de verhouding tussen de verandering in de optie prijs ten opzichte van een verandering in de onderliggende waarde registreert. Vervelend is echter dat deze verhouding niet constant is, met andere woorden, delta zelf is niet constant. Dat is ook niet zo verwonderlijk.
Beschouwen we een ver out of the money (OTM) calloptie. Als de onderliggende waarde stijgt zal dit aanvankelijk slechts een kleine rimpeling in de optiepremie veroorzaken, maar naarmate de onderliggende waarde blijft door stijgen en de optie minder out of the money geraakt zal meer van de stijging van de onderliggende waarde zijn weg vinden in de optiepremie. Met andere woorden, de delta zal toenemen.
Hoe de delta verandert als de onderliggende waarde verandert wordt nu gemeten door de gamma. Wiskundig geschoolde lezertjes zullen hier de tweede afgeleide in herkennen. We moeten overigens ook opmerken dat in het hier gehanteerde voorbeeld, van een alsmaar door stijgende onderliggende waarde, het erg waarschijnlijk is dat ook de geïmpliceerde volatiliteit van de onderliggende waarde toeneemt. Dit zal ook zijn (positieve) weerslag in de optiepremie hebben.
De gamma is dus het grootst voor at the money (ATM) opties en het kleinst voor zeer ver in, of out of the money opties. Als de gamma groot wordt houdt dit een risico in voor de optiebezitter, maar het kan ook extra rendement opleveren. Gamma’s kunnen erg groot worden voor opties vlak voor expiratie (helemaal op de expiratie dag zelf) voor at the money (ATM) opties, hetgeen doorgaans een heel leger aan dobbelende speculanten aantrekt.
De Rho
Dan hebben we nog de rho, maar heel relevant is deze niet, omdat dit een variabele is welke het risico meet van een veranderende rente. In de Black-Scholes optieforumule wordt een (risicoloze) rentevoet gebruikt ter berekening van theoretische optiewaarden, maar daar hoeven we ons hier niet persé mee te vermoeien.
Het is wel zo dat als de rente stijgt, de premie van call opties stijgt en die van put opties daalt. Het omgekeerde gebeurt met een rente daling. De rho meet met hoeveel de optiepremies stijgen of dalen bij veranderingen in de rente. Maar aangezien deze effecten klein zijn, vrijwel verwaarloosbaar klein in het huidige super lage renteklimaat, en de looptijd van de meeste optiestrategieën (weken of een paar maanden, doorgaans geen jaren) maken de effecten alleen maar minder belangrijk. Het moge duidelijk zijn dat de rho groter wordt naarmate de looptijd van de opties langer wordt.
Een kleine gids voor beleggen in opties
Wat volgt is een klein overzichtje van enige strategische implicaties van de verschillende waarde die de indicatoren kunnen aannemen.
Bijvoorbeeld: Een positieve delta wil zeggen dat u long bent in de onderliggende waarde, een positieve vega geeft aan dat u long volatiliteit bent, dat wil zeggen, uw optiepositie profiteert (stijgt in waarde) als de volatiliteit van de onderliggende waarde toeneemt. Een positieve theta wil zeggen dat uw optiepositie profiteert van een verloop van de tijdswaarde, en een positieve gamma geeft aan dat u netto long puts/calls bent. We gaan in gedetailleerdere artikelen nog uitgebreid in op deze materie.