De laatste parameter in ons Grieks alfabet is de gamma, en deze is gerelateerd aan de delta. Ter opfrissing van het geheugen, de delta meet de gevoeligheid van een optie van veranderingen in de onderliggende waarde. Preciezer omschreven geeft de delta de verandering weer als de onderliggende waarde $1 in waarde verandert.
Dat is erg handig om te weten, maar helaas zijn opties gecompliceerder en laten zij zich niet zomaar vangen in lineaire vergelijkingen. De delta heeft namelijk de irritante eigenschap om zelf te veranderen als de prijs van de onderliggende waarde verandert. Over kleine prijsveranderingen zijn deze effecten doorgaans klein, maar bij grote veranderingen gaat dit een rol spelen.
De gamma meet nu precies hoe de delta verandert, het is eigenlijk de tweede afgeleide van de vergelijking die de relatie tussen veranderingen in de koers van de optie als reactie op veranderingen in de onderliggende waarde bepaalt, maar we gaan u hier niet lastig vallen met wiskundige vergelijkingen. We pakken er weer een tabel bij om een en ander inzichtelijker te maken:
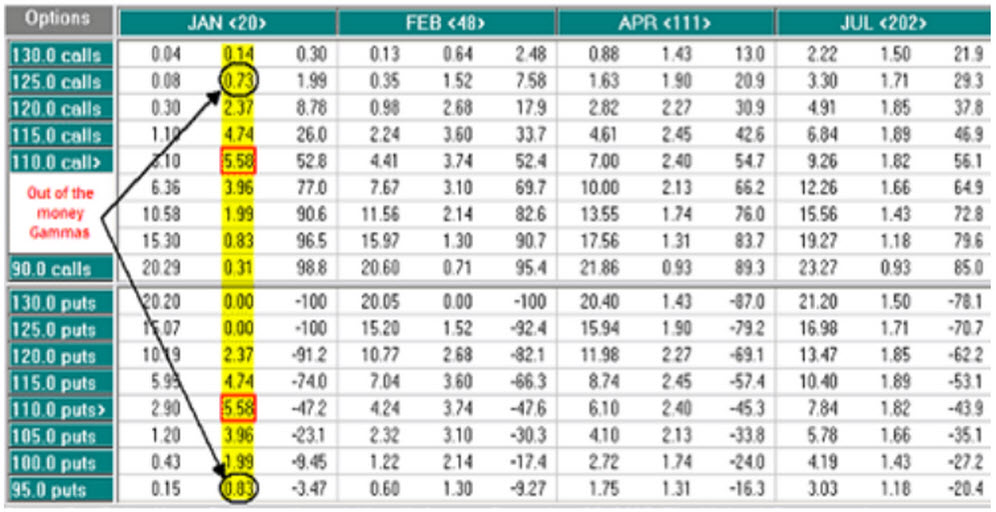
Oplettende lezertjes zullen weer de IBM opties herkennen die we ook in vorige artikelen hebben gebruikt. De datum is weer 29 december 2007, toen IBM aandelen $110,09 deden. De linker kolom geeft weer de uitoefenprijzen van de opties, de rechter kolommen de expiratiemaanden, waarbij de middelste kolom van iedere expiratiemaand de gamma waarden van de opties weergeeft.
Nemen we de januari opties (in het geel). Wat direct opvalt is dat de opties met een uitoefenprijs het dichtst bij de koers van de onderliggende waarde op dat moment ($110,09) de grootste gamma waarden hebben. Die van de Jan 110 calls, alsook die van de Jan 110 puts hebben dezelfde gamma waarde van 5,58.
Wat betekent dit nu? Dit betekent dat zowel het risico, maar ook het mogelijke rendement van de optie als gevolg van een verandering van de delta het grootst is voor at the money (ATM) opties. De relatie tussen de optieprijs en de onderliggende waarde is hier het minst lineair. De gamma is overigens wel altijd positief, omdat deze altijd met de delta mee verandert, dat wil zeggen, in dezelfde richting.
Wat ook opvalt is dat als de expiratiedatum verder weg ligt (voor een optie met dezelfde uitoefenprijs), de gamma verandert. Nemen we de out of the money (OTM) opties, de 125 call en de 95 put (weergegeven met pijlen in de figuur). Nemen we de 125 call dan zien we dat de gamma verandert van 0,73 in januari, tot 1,52 in februari, 1,90 in april, maar daalt tot 1.71 in juli. Voor de OTM puts is een vergelijkbare ontwikkeling te zien die u zelf in de tabel kunt aflezen.
Beleggen in opties: Delta en gamma
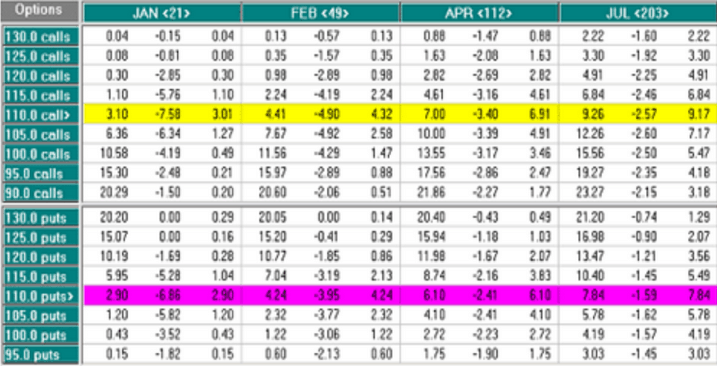
Het is ook inzichtelijk om te beschouwen hoe delta en gamma zich tot elkaar verhouden. Bezien we bijvoorbeeld de 115 OTM calls, dan kunnen we ook de delta waarden erbij betrekken, van de volgende tabel.
We zetten het overzichtelijk op een rijtje:
U ziet, naarmate de expiratiedatum verder weg is neemt de delta toe en de gamma af. Wat betekent het eigenlijk, een gamma van 4,74? Het betekent dat voor iedere $1 verandering in de onderliggende waarde zal de delta met 4,74 toenemen. Nemen we de januari 105 puts, dan zien we dat de delta 23,4 is en de gamma 3,96.
Stel dat u een put had gekocht en de onderliggende waarde (aandelen IBM) stijgen $5. Dan zou de Jan105 put ongeveer dezelfde waardes aan delta en gamma moeten hebben als de jan 110 put in de tabellen. De delta van de Jan105 put zou moeten veranderen met 5x de eigen gamma waarde, hetgeen 5 x 3,96 = 19,8 is. De delta wordt nu 23,4 + 19,8 = 43,2. Kijken we in de tabel dan lezen we af dat de Jan110 put een delta van 47,1 heeft, dat is toch een stukje groter.
Wat verklaart het verschil? U wilt het waarschijnlijk niet weten, maar ook de gamma zelf is niet constant. Om een preciezere berekening te maken zouden we eigenlijk de derde afgeleide van de vergelijking die de relatie tussen de onderliggende waarde en de optiepremie weergeeft, maar weest u gerust, dat gaan we u besparen.
Wat hebben we hier aan? De delta is een van de belangrijkste parameters van een optie, deze laat zien hoe de optiepremie reageert op veranderingen van de onderliggende waarde. Met name kopers van opties zien graag een hoge delta, wat betekent dat veel van de veranderingen van de onderliggende waarde ook in de optieprijs terecht komt.
Dat is natuurlijk meer naarmate opties minder out of the money, en meer in the money geraken, en ook een langere looptijd heeft doorgaans een gunstigere werking op de delta, simpel omdat er meer tijdswaarde in de optie zit. Maar het is belangrijk om te realiseren dat de delta zelf verandert, de gevoeligheid van de optieprijs voor veranderingen in de onderliggende waarde is niet constant.
Hoewel aanzienlijk minder belangrijk dan de delta zelf, is het soms ook wel handig om naar de verandering van de delta, ofwel de gamma te kijken. Zo kunnen twee optie (of optieposities) een min of meer gelijkwaardige delta hebben maar verschillen in de gamma. Als u de optie(combinatie) kiest met de laagste gamma, dan loopt u minder risico, maar verdient u ook minder rendement (bij dezelfde verandering van de onderliggende waarde).
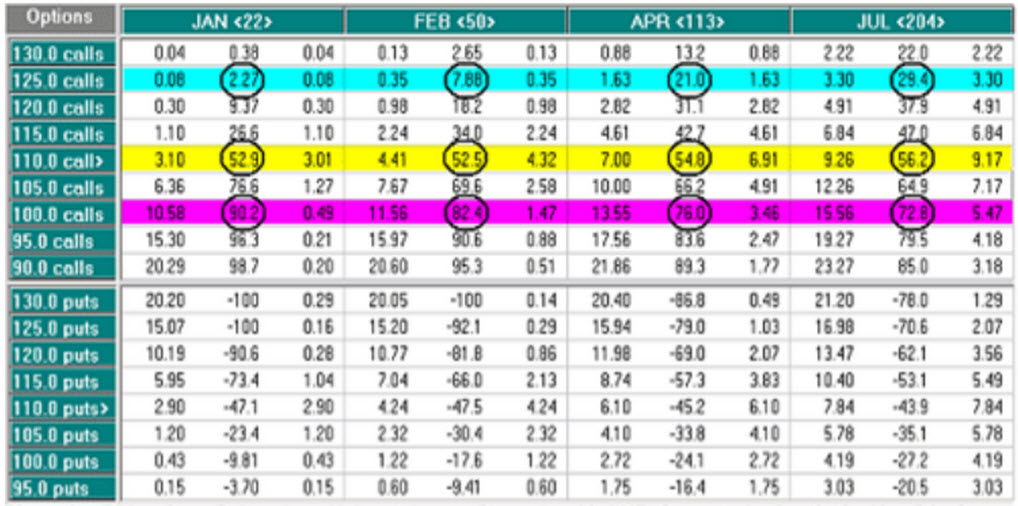
Tot besluit weer de bekendste optiestrategieën en de daarbij behorende waarde van de gamma. Voor de goede orde, een positieve gamma wil zeggen dat met een stijging van de onderliggende waarde de delta toeneemt, een negatieve gamma wil zeggen dat de delta afneemt.